ما هي المعادلات التفاضلية غير المتجانسة وأمثلة عليها
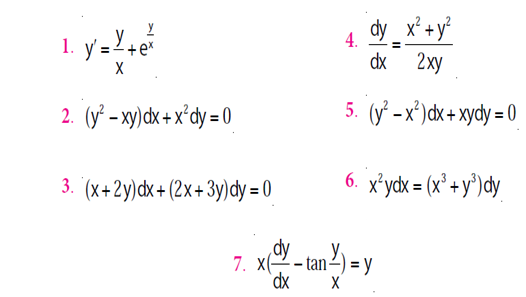
تُعد المعادلات التفاضلية جانبًا أساسيًا بكلٍ من علمي الفيزياء والرياضيات، وتقوم على عدد من القوانين الحسابية التي ربما تكون معقدة بعض الشيء ولكن حال استوعبها الطالب وفهم دواخل هذه المعادلات، فلن يجتهد بصعوبة للتعامل معها والوصول إلى الحل الصحيح، فمن خلال موقع منصتك نعرض لكم طرق حل المعادلات التفاضلية الغير متجانسة.
ما هي المعادلات التفاضلية غير المتجانسة وأمثلة عليها

كما تُعرف المعادلات التفاضلية الغير المتجانسة من الرتبة الأولى بأنها تحتوي على متغيرين فقط (س، ص)، فنكون المشتقة الأولى (د ص/ س) ولا توجد أية مشتقات أخرى أعلى منها بالمعادلة.
فيصير لدينا الشكل العام لقانون تلك المعادلات من الدرجة الأولى على النحو التالي: د ص/ دس + ص × ط(س) = ق(س)؛ حيث إن ط(س)، ق(س) هي دوال رياضية للمتغير س.
ففي حال تطلب الأمر لدى الطالب باستخدام هذا النوع من المعادلات التفاضلية (أي الدرجة الأولى)، يمكنه استخدام إما العامل المكامل، أو ثابت التباين، وسنوضح كلًا منهما فيما يلي:
أقرأ أيضًا: مسائل رياضيات مع الحل صعبة للأذكياء .. مميزات الرياضيات في حياتنا اليومية
1ـ طريقة حل المعادلات التفاضلية بالعامل المكامل
فعلى سبيل المثال: هذه المعادلة دص/دس – ص – س×هـ^س = 0، باستخدام العامل المكامل.
فلحل المسألة بشكل منطقي مُرتب، قم باتباع خطوات الحل التالية:
- قم بكتابة المعادلة على الصورة العامة لها: دص/دس – ص = س×هـ^س.
- نقوم بإيجاد العامل المكامل لها، حيث يكون ط(س) = -1؛ أي معامل ص.
- ك(س) = هـ^ ( ∫ (ط(س)× دس))
- ك(س) = هـ^ ( ∫ (-1× دس))
- ك(س) = هـ ^(- س)
- كما من خلال استخدامك الحل العام يصير معك:
- ص = ( ∫ ( ك(س)×ق(س)×دس + ج) / ك(س)؛ حيث أن ق(س) = س×هـ^س
- ص = ( ∫ ( هـ ^(- س)× س×هـ^س + ج) / هـ ^(- س)
- ص= ( ∫(س×دس +ج )) / هـ ^(- س)
- ص = هـ ^( س)× (( س^2/ 2 + ج))
أقرأ أيضًا: طرق حل المعادلات بخطوات سهلة على الطلاب
2ـ طريقة حل المعادلات التفاضلية عبر ثابت التباين
في حال استخدام تلك الطريقة لحل المعادلات التفاضلية، يُرجى الاطلاع جيدًا على المثال التالي:
تفكّر الآن وقم بحل المعادلة س×دص/دس = ص + 2×س^(3)، باستخدام طريقة ثابت التكامل، وسيأتي معنا حل هذه المسألة الرياضية على النحو التالي:
- قم بكتابة المعادلة المعطاة على صيغة معادلة تفاضلية متجانسة: دص/ دس + ص×ط(س) = 0
- قم بحل المعادلة من خلال الوصول لقيمة (ص)؛ وذلك لن يتم إلا بفصل المتغيرات.
- دص/ ص = دس/ س؛ وبتكامل الطرفين ينتج:
- لوهـ (ص) = لوهـ (س) + لوهـ (ج).
- ص = س×ج
- استبدل ج بدالة ج(س) لإيجاد حل المعادلة التفاضلية غير المتجانسة: ص = س×ج
- دص/ دس = جَ (س) ×س + ج(س)
- س× (جَ(س)×س + ج(س)) = ج(س)×س +2×س^(3)؛ تم استبدال (دص/ دس) و(ص) من المعادلة الأصلية بالمسألة.
- جَ(س) = 2س؛ وبتكامل الطرفين يصير: ج(س) = س^2 + ج1
- وبهذا يكون الحل النهائي للمسألة: ص = ج(س)×س
- ص = ( س^2 + ج1)×س
- ص = س^3 + س×ج1
أقرأ أيضًا: ما هي أهمية الإحصاء في البحث العلمي .. مراحل الإحصاء في البحث العلمي
وبهذا نكون تعرفنا معكم على تعريف تلخيصي للمعادلات التفاضلية غير المتجانسة، مع عرض أمثلة توضح كيفية استخدام قوانينها للوصول للحل الصحيح وفي وقت قياسي، ولكن الأمر يتوقف على مهارة عمل المعلم وإيصاله المعلومة للطالب، وأيضًا درجة اجتهاد الطالب ومحاولاته لفهمها والتدريب عليها مرارًا وتكرارًا.










